From Arithmetic to Algebra: Students’ Epistemological Obstacles

Abstract

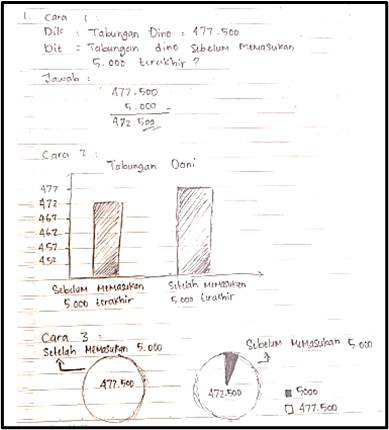
The initial algebraic concept typically introduced to students is the linear equation in one variable. One of the earliest difficulties students encounter with this concept is comprehending the significance of a variable. This study aims to investigate the epistemological obstacles faced by students in acquiring proficiency in linear equations in one variable. A qualitative phenomenological methodology was employed in this research. The participants consisted of 35 eighth-grade students enrolled in a junior high school who had previously studied linear equations in one variable. In the initial phase of the study, the researcher formulated two word problems. The utilization of word problems was intended to elucidate students’ thought processes in articulating their ideas or reasoning in written form. Subsequently, interviews were conducted with four selected students to corroborate the researcher’s interpretation of their written responses. The findings and discussion reveal that the conceptual deficiencies acquired during instruction contributed to the emergence of epistemological learning obstacles among students. This learning obstacle was identified through the solutions proposed by students, which were predominantly arithmetic rather than algebraic. Although the students acknowledged that the problem they were dealing with was related to the concept of linear equations in one variable, the majority still encountered difficulties in providing solutions in the form of a linear equation in one variable., particularly in the forms  and .